本文共 3947 字,大约阅读时间需要 13 分钟。
◆概念:js是一门在客户端进行交互的网页编程语言
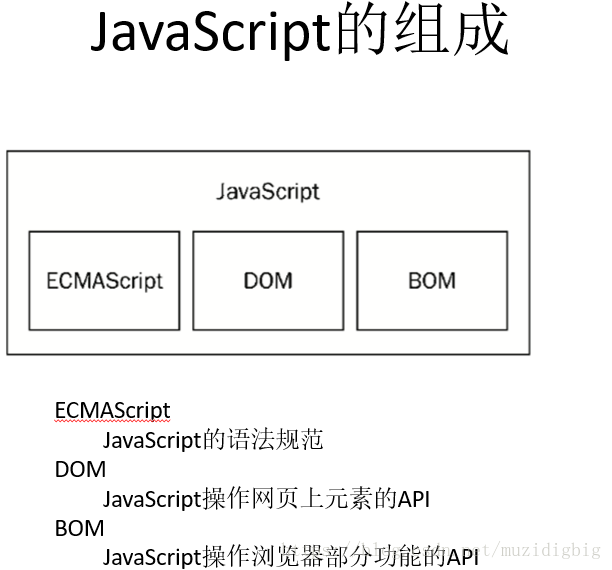
◆组成:
◎ecmascript js标准
◎dom 可以利用JS操作网页元素
◎Bom 通过api来操作浏览器
◆特点
简单易用
基于对象:与面向对象不同于没有封装、继承、多态。
基于过程:直接操作元素
解释执行: js引擎来执行源代码
编译执行: Java c# 源代码 ==>可执行文件.dll ==>电脑执行.dll课执行文件
◆使用范围:
表单验证
轮播图特效
游戏开发……
JavaScript的理解及作用
- JavaScript 被设计用来向 HTML 页面添加交互行为。
- JavaScript 是一种脚本语言(脚本语言是一种轻量级的编程语言)。
- JavaScript 由数行可执行计算机代码组成。
- JavaScript 通常被直接嵌入 HTML 页面。
- JavaScript 是一种解释性语言(就是说,代码执行不进行预编译)。
- 所有的人无需购买许可证均可使用 JavaScript。
- 区分大小写
- 每行结尾的分号可有可无(建议写上)
JavaScript 可以将动态的文本放入 HTML 页面:
类似于这样的一段 JavaScript 声明可以将一段可变的文本放入 HTML 页面:document.write("<h1>" + name + "</h1>")
JavaScript 可以对事件作出响应:
可以将 JavaScript 设置为当某事件发生时才会被执行,例如页面载入完成或者当用户点击某个 HTML 元素时。
JavaScript 可以读写 HTML 元素:
JavaScript 可以读取及改变 HTML 元素的内容。
JavaScript 可被用来验证数据:
在数据被提交到服务器之前,JavaScript 可被用来验证这些数据。
JavaScript 可被用来检测访问者的浏览器:
JavaScript 可被用来检测访问者的浏览器,并根据所检测到的浏览器,为这个浏览器载入相应的页面。
JavaScript 可被用来创建 cookies:
JavaScript 可被用来存储和取回位于访问者的计算机中的信息。
JavaScript的注册部分
ECMAScript:它是JavaScript的核心,包含(基本语法、变量、关键字、保留字、数据类型、语句、函数等等)
DOM:文档对象模型,包含(整个html页面的内容)
BOM:浏览器对象模型,包含(整个浏览器相关的内容)
JavaScript的实现
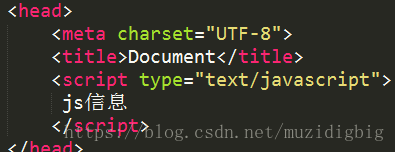
◆内嵌式写法(可嵌在html页面中的任意位置,建议最下面)
补充内嵌式写法:
推荐Js代码最好放在body结束标签的后边。
◆外链式写法(引入的方式引入到页面中)
HTML 的<script type="text/javascript" src="js代码路径">.... </script> 标签用于把外部 JavaScript 插入 HTML 页面中
◎新建一个js文件
◎通过script标签里的src=”1.js”属性将JS文件调入到当前页面。
补充外链式写法:推荐将多个js文件合并为一个js文件在浏览器中执行。
JavaScript语句的放置
1.位于 head 部分的脚本()
2.位于 body 部分的脚本(建议放在body之后)
3.外部 JavaScript(创建.js文件),需要通过下面的方式引入:<script src="xxx.js">....</script>
注意:外部文件不能包含 <script> 标签。
通常要在每行语句的结尾加上一个分号。
<script type="text/javascript">
window.onload = function () {
//此处为JavaScript代码
}
</script>
JavaScript 注释(与java类似)
单行的注释以 // 开始。
多行注释以 /* 开头,以 */ 结尾。
JavaScript 变量
JavaScript 变量名称的规则:
- 变量对大小写敏感(y 和 Y 是两个不同的变量)
- 变量必须以字母或下划线开始,其中变量名包含字母、数字、下划线、$
注释:由于 JavaScript 对大小写敏感,变量名也对大小写敏感。
通过 var 语句来声明 JavaScript 变量(js变量的声明只能用var):
变量名在 = 符号的左边,而需要向变量赋的值在 = 的右侧。
var x; var carname="Volvo";
标识符:用户自定义的所有名字叫做标识符。即变量名
不要在后续的代码中改变数据类型
//变量的声明var 变量名; //JavaScript变量可以不声明,直接使用。默认值:undefined//变量的赋值var 变量名 = 值; // JavaScript变量是弱类型,给它什么类型的值它就是什么类型,即同一个变量可以存放不同类型的数据
在函数内变量未被声明则为全局变量
变量的作用范围:
全局变量在方法体外
局部变量在方法体内声明的变量(形参,函数内声明的变量)函数调用完变量销毁
JavaScript 数据类型(变量类型)
var s1=null; 表示变量值为空,该变量在内存中是不存在的。真正的空。 s1的数据类型为 object
通过typeof(变量) 进行数据类型的判断
Var s1=123;
alert(typeof(s1)); //number类型数组/对象;获取它的数据类型返回的都是一个对象类型(数组也可看成一个对象)
数组(数组的索引是从0开始):
var cars=new Array();
cars[0]="Saab"; cars[1]="Volvo";cars[2]="BMW";
或:var cars=new Array("Saab","Volvo","BMW");
或:var cars=["Saab","Volvo","BMW"];
对象(对象由花括号分隔。在括号内部,对象的属性以名称和值对的形式 (name : value) 来定义。属性由逗号分隔):
var person={
firstname : "John", lastname : "Doe", id : 5566};
获取对象中的值:name=person.lastname;
name=person["lastname"];
JavaScript的消息框(以弹出窗口的形式显示)
1.alert("文本") 警告框
警告框经常用于确保用户可以得到某些信息。
当警告框出现后,用户需要点击确定按钮才能继续进行操作。
2.confirm("文本") 确认框
确认框用于使用户可以验证或者接受某些信息。
当确认框出现后,用户需要点击确定或者取消按钮才能继续进行操作。
3.prompt("文本","默认值") 提示框
提示框经常用于提示用户在进入页面前输入某个值。
当提示框出现后,用户需要输入某个值,然后点击确认或取消按钮才能继续操纵。
4.window.open("打开html页面的路径","新窗口中打开_blank");新窗口中打开页面
5.window.close();关闭窗口
JavaScript 的网页输出
1.alert("文本") 警告框
2.document.write("文本") 直接向浏览器中写入内容(不仅可以输出内容,还可以输出html标签。)
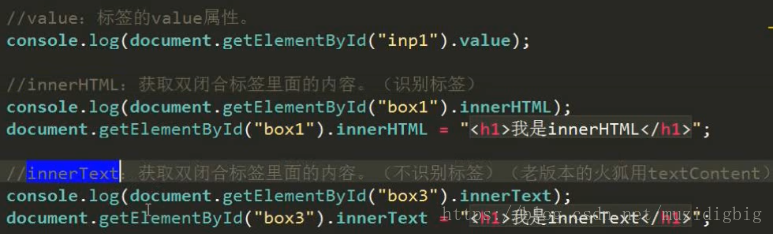
3.document.getElementById(id).innerHTML="文本" 向页面指定位置写入内容
4.console.log() 在控制要打印出内容(typeof()/typeof 打印数据类型)
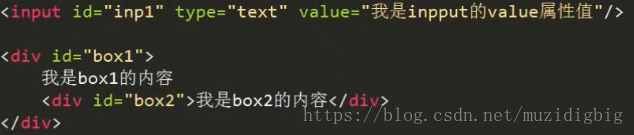
value和innerHTML和innerText和textContent
1.老版本的火狐不支持innerText;IE678不支持textContent
2.p不能嵌套p。h1不能嵌套h1。a连接内部不能嵌套a连接
操作节点内容(文本)兼容性好,也可输出html标签,但是会覆盖原来的文本
更改节点内容:对象.innerHtml=”节点输出内容”
获取节点内容:对象.innerHtml
JavaScript的运算符
+、-、*、/、%
加运算:
★两个数据类型都为数字类型变量相加,得到的是数字类型。
★一个为数字类型的变量和一个为字符串类型的变量相加,得到的是一个字符串类型,加号起一个连接的作用。
减运算
★如果两个变量都为数字类型相减,得到的是数字类型。
★如果一个为数字类型的变量,一个为数字字符串,相减得到的是数字类型。
★如果一个为数字类型的字符串,一个为非数字字符串,相减得到NaN。
NaN: not a number
★两个都为字符串的变量相减,得到的是NaN。
除运算
★两个都为数字类型的变量,相除得到的是数字类型。
★如果一个为数字类型的变量,一个为数字字符串变量,相除得到的是数字类型。
★如果一个为数字类型的变量,一个为非数字字符串,相除得到的NaN。
★如果0作为除数,得到的是infinity(无限大),是一个数字类型。
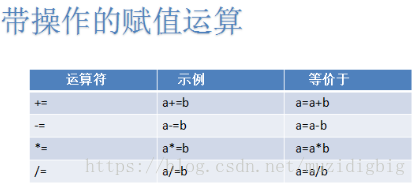
赋值运算符
JavaScript 循环(控制结构)
for 将一段代码循环执行指定的次数
while 当指定的条件为 true 时循环执行代码(不知道循环的次数)
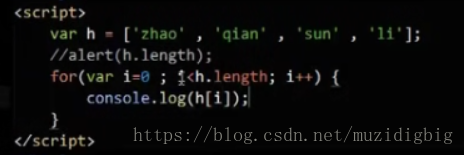
JavaScript For...In 声明
For...In 声明用于对数组或者对象的属性进行循环操作。
for ... in 循环中的代码每执行一次,就会对数组的元素或者对象的属性进行一次操作。
如有问题请多多谅解!希望给您带来帮助!祝您生活愉快。